Tập lồi (convex sets)
Affine set
đường thẳng: đi qua hai đểm $x_{1}, x_{2}$
$$ x=\theta x_{1}+(1-\theta) x_{2} \quad(\theta \in \mathbf{R}) $$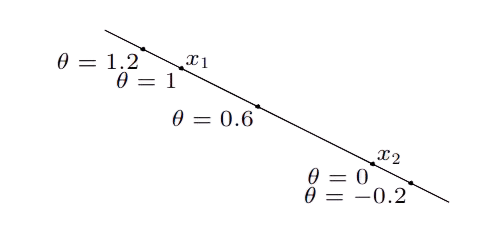
tập hợp affine: chứa đường thẳng đi qua hai điểm phân biệt bất kỳ trong tập hợp
ví dụ: tập nghiệm của phương trình tuyến tính $\{x \mid A x=b\}$
(ngược lại, mọi tập hợp affine có thể được biểu diễn dưới dạng tập nghiệm của hệ phương trình tuyến tính)
Tập lồi
đoạn thẳng: giữa hai đểm $x_{1}, x_{2}$
$$ x=\theta x_{1}+(1-\theta) x_{2} $$với $0 \leq \theta \leq 1$
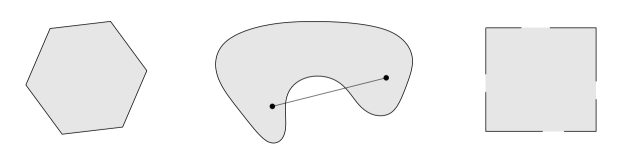
tập lồi: chứa đoạn thẳng giữa hai điểm bất kỳ trong tập hợp
$$ x_{1}, x_{2} \in C, \quad 0 \leq \theta \leq 1 \quad \Longrightarrow \quad \theta x_{1}+(1-\theta) x_{2} \in C $$ví dụ: (một tập hợp lồi, hai tập hợp không lồi)
Tổ hợp lồi và bao lồi
tổ hợp lồi (Convex combination): của $x_{1}, \ldots, x_{k}:$ là bất kỳ điểm $x$ của hình thức
$$ x=\theta_{1} x_{1}+\theta_{2} x_{2}+\cdots+\theta_{k} x_{k} $$với $\theta_{1}+\cdots+\theta_{k}=1, \theta_{i} \geq 0$
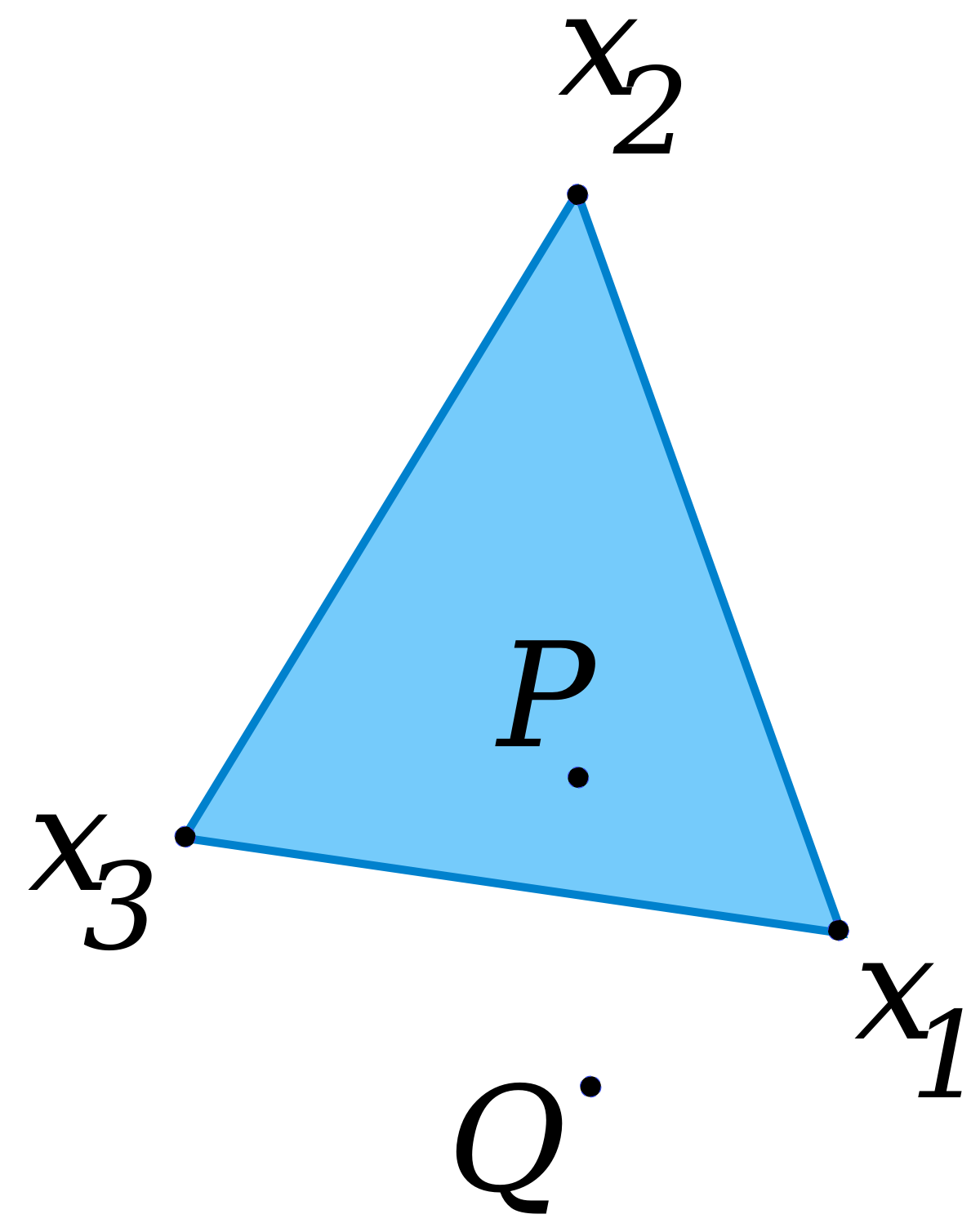
$P$ thuộc tổ hợp lồi của $x_1, x_2, x_3$ còn $Q$ thì không
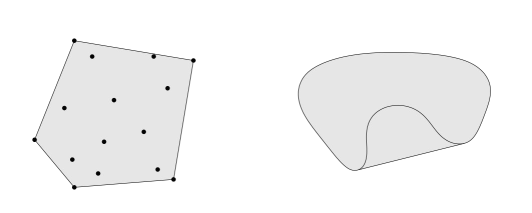
bao lồi (convex hull, conv $S$): tập hợp lồi nhỏ nhất chứa $S$
Nón lồi
tổ hợp lồi không âm:(conic nonnegative combination) của $x_{1} và x_{2}$ là bất kỳ điểm $x$ của hình thức
$$ x=\theta_{1} x_{1}+\theta_{2} x_{2} $$với $\theta_{1} \geq 0, \theta_{2} \geq 0$

hình nón lồi:(convex cone) tập hợp chứa tất cả các tổ hợp hình nón của các điểm trong tập hợp


Siêu phẳng và nửa không gian
siêu phẳng:tập hợp của hình thức $\left\{x \mid a^{T} x=b\right\}(a \neq 0)$
Trong không gian Euclid $n$ chiều, siêu phẳng là khái niệm mở rộng của mặt phẳng lên thành $n-1$ chiều. Ví dụ, trong không gian 3 chiều, siêu phẳng chính là mặt phẳng 2 chiều. Trong không gian 2 chiều, siêu phẳng là đường thẳng 1 chiều. Siêu phẳng tách đôi không gian.

nửa không gian:tập hợp của hình thức $\left\{x \mid a^{T} x \leq b\right\}(a \neq 0)$

hình nón lồi:(convex cone) tập hợp chứa tất cả các tổ hợp hình nón của các điểm trong tập hợp
- $a$ là vectơ pháp tuyến
- siêu mặt phẳng là affine và lồi; nửa không gian lồi
Euclidean balls và ellipsoids
(Euclidean) ball với tâm $x_{c}$ và bán kính $r$
$$ B\left(x_{c}, r\right)=\left\{x \mid\left\|x-x_{c}\right\|_{2} \leq r\right\}=\left\{x_{c}+r u \mid\|u\|_{2} \leq 1\right\} $$ellipsoid: tập hợp có dạng
$$ \left\{x \mid\left(x-x_{c}\right)^{T} P^{-1}\left(x-x_{c}\right) \leq 1\right\} $$với $P \in \mathbf{S}_{++}^{n}($i.e., $P$ symmetric positive definite)
đại diện khác: $\left\{x_{c}+A u \mid\|u\|_{2} \leq 1\right\}$ với A square và nonsingular
Tham khảo:
Norm balls và norm cones
norm: một function $\|\cdot\|$ thỏa mãn
- $\|x\| \geq 0 ;\|x\|=0$ nếu và chỉ nếu $x=0$
- $\|t x\|=|t|\|x\|$ với $t \in \mathbf{R}$
- $\|x+y\| \leq\|x\|+\|y\|$
ký hiệu: $\|\cdot\|$ là chung chung (không xác định) của norm; $\|\cdot\|_{\text {symb }}$ là trường hợp cụ thể của norm
norm ball với tâm $x_{c}$ và bán kính $r:\left\{x \mid\left\|x-x_{c}\right\| \leq r\right\}$
norm cone: $\{(x, t) \mid\|x\| \leq t\}$
Khối đa diện
tập nghiệm của nhiều bất phương trình tuyến tính và phương trình bằng nhau (siêu phẳng)
$$ A x \preceq b, \quad C x=d $$$\left(A \in \mathbf{R}^{m \times n}, C \in \mathbf{R}^{p \times n}, \preceq\right.$ là bất bình đẳng từng thành phần$)$
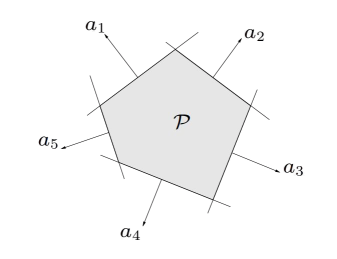
đa diện là giao của một số hữu hạn các nửa không gian và siêu mặt phẳng
Positive semidefinite cone
ký hiệu:
- $\mathbf{S}^{n}$ tập hợp $n \times n$ matrix đối xứng
- $\mathbf{S}_{+}^{n}=\left\{X \in \mathbf{S}^{n} \mid X \succeq 0\right\}$ : positive semidefinite $n \times n$ matrices $$ X \in \mathbf{S}_{+}^{n} \Longleftrightarrow z^{T} X z \geq 0 \text { for all } z $$ $\mathbf{S}_{+}^{n}$ là một hình nón lồi
- $\mathbf{S}_{++}^{n}=\left\{X \in \mathbf{S}^{n} \mid X \succ 0\right\}$ : positive definite $n \times n$ matrices
ví dụ: $X=\left[\begin{array}{ll}x & y \\ y & z\end{array}\right] \in \mathbf{S}_{+}^{2} \Longleftrightarrow x \geq 0, \quad z \geq 0, \quad x z \geq y^{2}$

Các phép toán bảo toàn độ lồi
các phương pháp thực tế để xác định độ lồi của một tập hợp $C$
- áp dụng định nghĩa: $$ x_{1}, x_{2} \in C, \quad 0 \leq \theta \leq 1 \quad \Longrightarrow \quad \theta x_{1}+(1-\theta) x_{2} \in C $$
-
chỉ ra rằng $C$ nhận được từ các tập lồi đơn giản (siêu phẳng, nửa không gian, norm balls,...) bằng các phép toán bảo toàn độ lồi
- intersection
- affine functions
- perspective function
- linear-fractional functions
Intersection
giao của (bất kỳ số lượng) tập lồi là lồi
Affine function
giả sử $f: \mathbf{R}^{n} \rightarrow \mathbf{R}^{m}$ là affine $\left(f(x)=A x+b\right.$ với $\left.A \in \mathbf{R}^{m \times n}, b \in \mathbf{R}^{m}\right)$ khi đó
- ảnh của một tập lồi dưới $f$ là tập lồi $$ S \subseteq \mathbf{R}^{n} \text { convex } \Longrightarrow f(S)=\{f(x) \mid x \in S\} \text { convex } $$
- ảnh nghịch đảo ảnh $f^{-1}(C)$ của một tập lồi dưới $f$ là lồi $$ C \subseteq \mathbf{R}^{m} \text { convex } \Longrightarrow f^{-1}(C)=\left\{x \in \mathbf{R}^{n} \mid f(x) \in C\right\} \text { convex } $$
ví dụ: scaling, translation, projection
Perspective và hàm phân số tuyến tính
perspective function $P: \mathbf{R}^{n+1} \rightarrow \mathbf{R}^{n}$ $$ P(x, t)=x / t, \quad \operatorname{dom} P=\{(x, t) \mid t>0\} $$
ảnh và ảnh nghịch đảo của tập lồi dưới perspective là tập lồi
hàm phân số tuyến tính$f: \mathbf{R}^{n} \rightarrow \mathbf{R}^{m}$ $$ f(x)=\frac{A x+b}{c^{T} x+d}, \quad \operatorname{dom} f=\left\{x \mid c^{T} x+d>0\right\} $$
ảnh và ảnh nghịch đảo của tập lồi theo hàm phân số tuyến tính là lồi
Bất bình đẳng tổng quát
giao của (bất kỳ số lượng) tập lồi là lồi
Intersection
giao của (bất kỳ số lượng) tập lồi là lồi
Intersection
giao của (bất kỳ số lượng) tập lồi là lồi